This project is an exemplary application of fuzzy logic for controlling different types of processes. I wrote it for an Artificial Intelligence course in Windesheim University of Applied Sciences. The assignment is composed of four components:
- Knowledge base
- Knowledge base parser
- Fuzzy Logic Controler
- Controlled process
Knowledge base
It is a set of rules and constraints, describing a given process, defined in Bacus-Naur form:
<knowledge base> ::= KB <universe list>
<variable list> <rule list>
KB_END
<universe list> ::= <universe> { <universe> }
<universe> ::= UNIVERSE
<universe name> <set list>
UNIVERSE_END
<set list> ::= <set> { <set> }
<set> ::= SET <set name>
<x1> <x2> <x3> <x4>
SET_END
<variable list> ::= <variable> { <variable> }
<variable> ::= VARIABLE <variable name>
<universe name> <variable type>
VARIABLE_END
<variable type> ::= in | out
<rule list> ::= <rule> { <rule> }
<rule> ::= RULE <rule name>
IF <premisse> THEN <conclusion>
RULE_END
<premisse> ::= <expression>
<conclusion> ::= <simple expression>
<expression> ::= <term> { OR <term> }
<term> ::= <factor> { AND <factor> }
<factor> ::= <simple expression> |
NOT <factor> | ( <expression> )
<simple expression> ::= <variable name> IS <set name>
<set name> ::= <name>
<variable name> ::= <name>
<universe name> ::= <name>
<rule name> ::= <name>
<x1> ::= <double>
<x2> ::= <double>
<x3> ::= <double>
<x4> ::= <double>
<name> ::= <letter or underscore>
{ <letter or underscore> | <digit> }
<letter or underscore> ::= <letter> | _
<letter> ::= a..z | A .. Z
<digit> ::= 0 .. 9
<double> ::= <signed double> | <unsigned double>
<signed double> ::= - <unsigned double>
<unsigned double> ::= <number> |
<number> . <number>
<number> ::= <digit> { <digit> }
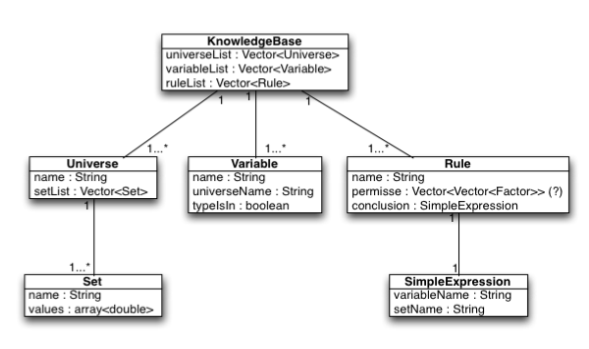
In general our knowledge base implementation has a tree-based structure in
which different levels of parsed data are stored. The figure below defines the relationships and connections between elements.
Parser
The parsing process is divided into two subprocesses. The first one analyzes the structure of knowledge base, the second is concerned with evaluation of expressions. Parsing of knowledge base may be depicted in steps as follows:
- Knowledge base file is read and stored in a vector data structure
- The structure is parsed starting from the most general tags. This way the input text is divided step by step, taking into account the tags: kb, universe, variable, rule. After a part of input is matched by a regular expression, it is being processed. The file structure is verified. The set of functions used for this purpose has a ‘parse’ prefix, (i.e. parseKB(), parseUniverse()).
- If a part of text is matched by a ‘parse’ function, the ‘process’ function is invoked. The set of functions with ‘process’ prefix analyzes the contents of every block matched by the previous phase. For example, if a RULE block has been found, it is being verified and a rule with read data is added to a structure named KB. This structure is composed of three separate vectors: for universes, variables and rules. Every time one of these blocks is encountered, it is added to the structure.
-
The synchronization between ‘parse’ phase and ‘process’ phase is done by statemanager. This is a stack-based class, that keeps parser informed about the block it is currently parsing and how ‘deep’ in the structure of knowledge base it currently works. In other words, if a significant block is
matched by ‘parse’ phase and the data is passed to ‘process’ phase, the current state is pushed onto a stack. When processing is finished, the state is popped from the stack.
- When parsing rules, the second subprocess of parsing is used. Since the conclusion part may be only a simple_expression, it is obviously added to KB structure. However, the premisse part may be very simple or incomparably more complex. The evaluation of premisse is preformed by a top-down parser.
-
Top-down parsing is a strategy of analyzing unknown data relationships by hypothesizing general parse tree structures and then considering whether the known fundamental structures are compatible with the hypothesis. In our case, the expression can be analyzed according to the given grammar.
Firstly, the expression is scanned in search of OR statements and, according to the position of brackets, divided into smaller parts. This process is complex and does not use regular expression matching as the result it involves character by character check. The similar scanning is
performed in case of AND statements. The functions separatemajorORs() and separatemajorANDs() are responsible for this.
- In this part of the parsing process some additional tasks are performed, like removing brackets from the expressions or negating the factors.
-
In next step all terms and factors are analyzed. Finally, all the simple expressions, that were found, are added to KB structure. The results of the parsing process are passed to Knowledge Base
representation from which they are accessible to the Fuzzy Logic Controller.
Fuzzy Logic Controller
FLC uses the data gained in the parsing process. It evaluates every rule from the knowledge base. First, the premise is evaluated and the membership to a given fuzzy set is assigned. In case of complex premises, when OR operator is used the maximum value of two simple premises is taken into account, for the AND operator the minimum value would be taken. This process is described as fuzzification stage. Next, the decision making process itself begins. The conclusion provides FLC with a fuzzy set, that should be clipped at the value acquired from premise.
All the clipped fuzzy sets from analyzed rules are combined and the process advances to defuzzification stage. The defuzzification stage is based on calculating the point of gravity of the fuzzy set combined form all the clipped sets from decision making stage. The result of the defuzzification phase is passed to the controlled process.
Controller Processes
In this exemplary application two processes can be controlled:
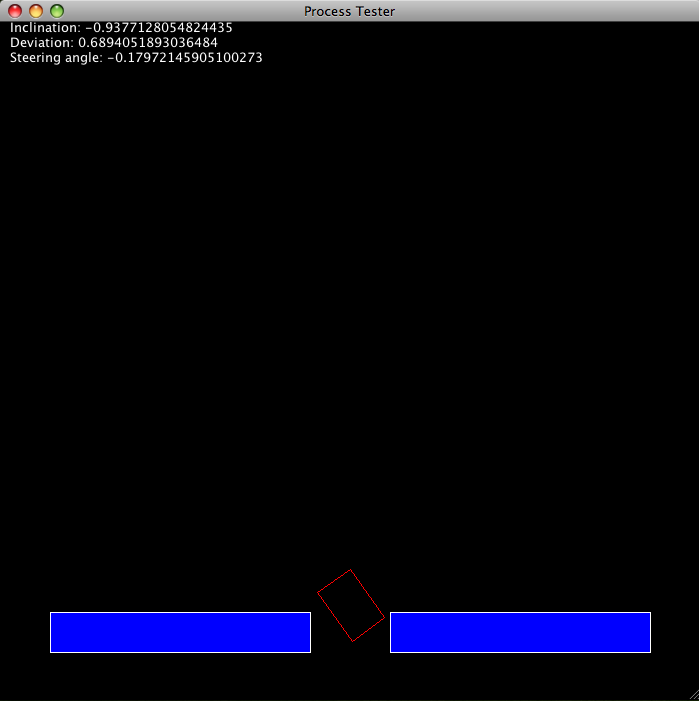
- Vehicle steering – controlling a small cart and leading it into a gateway. Exemplary knowledge base: kb_car.txt
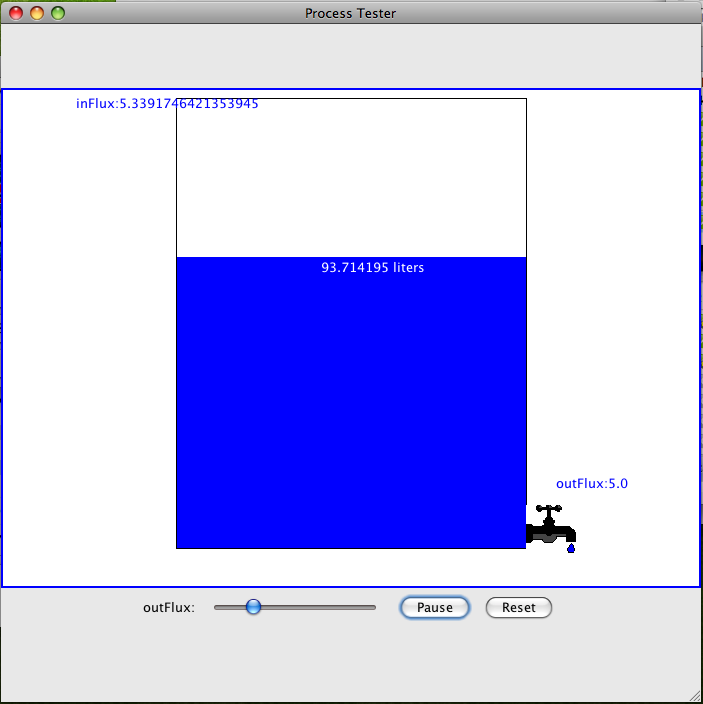
- Water tank – controlling level of water in a tank. Exemplary knowledge base: kb_tank.txt
However, it should be rather easy to plugin arbitrary complex process implementing the same API.
Application can be downloaded from here:
fuzzything.zip